las metematicas y nuestro entorno: 2011

proyecto

Un proyecto es una planificación que consiste en un conjunto de actividades que se encuentran interrelacionadas y coordinadas;¹ la razón de un proyecto es alcanzar objetivos específicos dentro de los límites que imponen un presupuesto, calidades establecidas previamente y un lapso de tiempo previamente definido.¹ La gestión de proyectos es la aplicación de conocimientos, habilidades, herramientas y técnicas a las actividades de un proyecto para satisfacer los requisitos del proyecto.²

Un proyecto consiste en reunir varias ideas para llevarlas a cabo, es un emprendimiento que tiene lugar durante un tiempo limitado, y que apunta a lograr un resultado único. Surge como respuesta a una necesidad, acorde con la visión de la organización, aunque ésta puede desviarse en función del interés. El proyecto finaliza cuando se obtiene el resultado deseado, y se puede decir que colapsa cuando desaparece la necesidad inicial, o se agotan los recursos disponibles.

• La capacidad de prestar un servicio como, por ejemplo, las funciones del negocio que respaldan la producción o la distribución

• Un resultado como, por ejemplo, salidas o documentos. Por ejemplo, de un proyecto de investigación se obtienen conocimientos que pueden usarse para determinar si existe o no una tendencia o si un nuevo proceso beneficiará a la sociedad.

La singularidad es una característica importante de los productos entregables de un proyecto. Por ejemplo, se han construido muchos miles de edificios de oficinas, pero cada edificio individual es único: diferente propietario, diferente diseño, diferente ubicación, diferente contratista, etc. La presencia de elementos repetitivos no cambia la condición fundamental, única de manejo y propósitos de un proyecto.

Elaboración gradual

La elaboración gradual es una característica de los proyectos que acompaña a los conceptos de temporal y único. “Elaboración gradual” significa desarrollar en pasos e ir avanzando mediante incrementos. Por ejemplo, el alcance de un proyecto se define de forma general al comienzo del proyecto, y se hace más explícito y detallado a medida que el equipo del proyecto desarrolla un mejor y más completo entendimiento de los objetivos y de los productos entregables. La elaboración gradual no debe confundirse con la corrupción del alcance.

Tipos de proyectos

Un proyecto también es un esfuerzo temporal que se lleva a cabo para crear un producto, servicio o resultado único.

Existen múltiples clasificaciones de los proyectos, una de ellas los considera como productivos y públicos.⁴

Proyecto productivo: Son proyectos que buscan generar rentabilidad económica y obtener ganancias en dinero. Los promotores de estos proyectos suelen ser empresas e individuos interesados en alcanzar beneficios económicos para distintos fines.
Proyecto público o social: Son los proyectos que buscan alcanzar un impacto sobre la calidad de vida de la población, los cuales no necesariamente se expresan en dinero. Los promotores de estos proyectos son el estado, los organismos multilaterales, las ONG y también las empresas, en sus políticas de responsabilidad social.

Otras formas de realizar la clasificación de los proyectos son las siguientes:

Basándose en el contenido del proyecto
- Proyectos de construcción
- Proyectos de Informática
- Proyectos empresariales
- Proyectos de desarrollo de productos y servicios
Basándose en la organización participante
- Proyectos Internos
- Proyectos de departamento
- Proyectos de unidades cruzadas
- Proyectos externos (de imagen corporativa)
Basándose en la complejidad
- Proyectos Simples
- Proyectos complejos
- Proyectos técnicos
- Programas
- Mega proyectos
- Proyectos científicos
- Proyectos de vida
- Proyectos escolares.

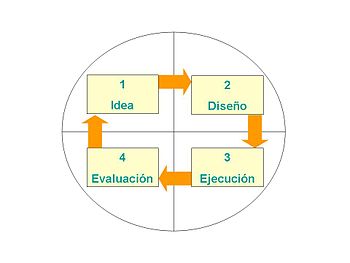
Etapas de un proyecto

Ciclo de un proyecto.

La idea de proyecto: Que consiste en establecer la necesidad u oportunidad a partir de la cual es posible iniciar el diseño del proyecto. La idea de proyecto puede iniciarse debido a alguna de las siguientes razones:¹
- Porque existen necesidades insatisfechas actuales o se prevé que existirán en el futuro si no se toma medidas al respecto.
- Porque existen potencialidades o recursos subaprovechados que pueden optimizarse y mejorar las condiciones actuales.
- Porque es necesario complementar o reforzar otras actividades o proyectos que se producen en el mismo lugar y con los mismos involucrados.

Diseño: Etapa de un proyecto en la que se valoran las opciones, tácticas y estrategias a seguir, teniendo como indicador principal el objetivo a lograr. En esta etapa se produce la aprobación del proyecto, que se suele hacer luego de la revisión del perfil de proyecto y/o de los estudios de pre-factibilidad, o incluso de factibilidad. Una vez dada la aprobación, se realiza la planificación operativa, un proceso relevante que consiste en prever los diferentes recursos y los plazos de tiempo necesarios para alcanzar los fines del proyecto, asimismo establece la asignación o requerimiento de personal respectivo.

Ejecución: Consiste en poner en práctica la planificación llevada a cabo previamente.

Evaluación. Etapa final de un proyecto en la que éste es revisado, y se llevan a cabo las valoraciones pertinentes sobre lo planeado y lo ejecutado, así como sus resultados, en consideración al logro de los objetivos planteados.

Documentación de un proyecto

1 Importancia.

2 Informe técnico del proyecto.

2.1 Plan estructurado del proyecto. (Marco Lógico)

2.2 Plan de control de personal.

2.3 Otros planes.

2.4 Manejo de recursos.

3 Informe administrativo.

3.1 Plan organizacional del proyecto.

3.2 Plan de gastos / plazos.

3.3 Plan de actividades del personal.

3.4 Plan de gestión de riesgos.

3.5 Otros planes.

4 Manuales de un proyecto.

4.1 Manual técnico.

4.2 Manual de usuario.

4.3 Manual administrativo.

maximos y minimos

En matemáticas, los máximos y mínimos de una función, conocidos colectivamente como extremos de una función, son los valores más grandes (máximos) o más pequeños (mínimos), que toma una función en un punto situado ya sea dentro de una región en particular de la curva (extremo local) o en el dominio de la función en su totalidad (extremo global o absoluto).¹ ² ³ De manera más general, los máximos y mínimos de un conjunto (como se define en teoría de conjuntos) son los elementos mayor y menor en el conjunto, cuando existen. El localizar valores extremos es el objetivo básico de la optimización matemática.

Extremos relativos o locales

Sea $f(x): A\sub\mathbb{R} \longrightarrow \mathbb {R}$ , sea $x_0 \in A$ y sea $P\,(x_0, f(x_0))$ un punto perteneciente a la función.

Se dice que

p

es un máximo local de

f

si existe un entorno reducido de centro

x 0

, en símbolos

E'(x 0)

, donde para todo elemento

x

E'(x 0)

se cumple $f(x) \le f(x_0)$ . Para que esta propiedad posea sentido estricto debe cumplirse

f (x) < f (x 0)

Análogamente se dice que el punto

p

es un mínimo local de

f

si existe un entorno reducido de centro

x 0

, en símbolos

E'(x 0)

, donde para todo elemento

x

E'(x 0)

se cumple $f(x) \ge f(x_0)$ .

[editar]Extremos absolutos

Sea $f(x): A\sub\mathbb{R} \longmapsto \mathbb {R}$ , sea $x_0 \in A$ y sea $P\,(x_0, f(x_0))$ un punto perteneciente a la función.

Se dice que P es un máximo absoluto de f si, para todo x distinto de

x 0

pertenenciente al subconjunto A, su imagen es menor o igual que la de

x 0

. Esto es:

$P\,(x_0, f(x_0))$ máximo absoluto de $f \iff \forall x \ne x_0, x \in A, f(x_0) \ge f(x)$ .

Análogamente, P es un mínimo absoluto de f si, para todo x distinto de

x 0

pertenenciente al subconjunto A, su imagen es mayor o igual que la de

x 0

. Esto es:

$P\,(x_0, f(x_0))$ mínimo absoluto de $f \iff \forall x \ne x_0, x \in A, f(x_0) \le f(x)$ .

formulas de derivadas

En las fórmulas siguientes se considera que $x,a,b,k \in \mathbb{R}, n \in \mathbb{N}$ :

$f\left(x\right) = a$	$f'\left(x\right) = 0$
$f\left(x\right) = x$	$f'\left(x\right) = 1$
$f\left(x\right) = ax$	$f'\left(x\right) = a$
$f\left(x\right) = ax + b$	$f'\left(x\right) = a$
$f\left(x\right) = x^n$	$f'\left(x\right) = nx^{n-1}$
$f\left(x\right) = \sqrt{x}$	$f'\left(x\right) = \frac{1}{2\sqrt{x}}$
$f\left(x\right) = e^x$	$f'\left(x\right) = e^x$
$f\left(x\right) = \ln(x)$	$f'\left(x\right) = \frac{1}{x}$
$f\left(x\right) = a^x (a >0)$	$f'\left(x\right) = a^x \ln(a)$
$f\left(x\right) = \log_{b}(x)$	$f'\left(x\right) = \frac{1}{x\ln(b)}$
$f\left(x\right) = \frac{1}{x^n} = x^{-n}$	$f'\left(x\right) = -nx^{-n-1} = \frac{-n}{x^{n+1}}$
$f\left(x\right) = \operatorname{sen}(x)$	$f'\left(x\right) = \cos(x)$
$f\left(x\right) = \cos(x)$	$f'\left(x\right) = -\operatorname{sen}(x)$
$f\left(x\right) = \tan(x)$	$f'\left(x\right)=\sec^2(x)=\frac{1}{cos^2(x)}=1+\tan^2(x)$
$f\left(x\right) = \csc(x)$	$f'\left(x\right) = -\csc(x)\cot(x)$
$f\left(x\right) = \sec(x)$	$f'\left(x\right) = \sec(x)\tan(x)$
$f\left(x\right) = \cot(x)$	$f'\left(x\right) = -\csc^2(x)$
$f\left(x\right) = \operatorname{arcsen}(x)$	$f'\left(x\right) = \frac{1}{\sqrt{1-x^2}}$
$f\left(x\right) = \arccos(x)$	$f'\left(x\right) = \frac{-1}{\sqrt{1-x^2}}$
$f\left(x\right) = \arctan(x)$	$f'\left(x\right) = \frac{1}{1+x^2}$
$f\left(x\right) = g(x) \pm h(x)$	$f'\left(x\right) = g'(x) \pm h'(x)$
$f\left(x\right) = g(x) \cdot h(x)$	$f'\left(x\right) = g'(x) \cdot h(x) + g(x) \cdot h'(x)$
$f\left(x\right) = k \cdot g(x)$	$f'\left(x\right) = k \cdot g'(x)$
$f\left(x\right) = \frac{g(x)}{h(x)}$	$f'\left(x\right) = \frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{h^2(x)}$
$f\left(x\right) = g\left(x\right)^{h\left(x\right)}$	$f'\left(x\right) = h\left(x\right) \cdot g'\left(x\right) \cdot g\left(x\right)^{\left(h\left(x\right)-1\right)} + g\left(x\right)^{h\left(x\right)} \cdot h'\left(x\right) \cdot ln\left(g\left(x\right)\right)$
$f\left(x\right) = g \circ h = g(h(x))$	$f'\left(x\right) = (g'\circ h) \cdot h' = g'(h(x)) \cdot h'(x)$

viernes, 2 de diciembre de 2011